Enigmes de la semaine des Mathématiques 2016 publié le 08/04/2016
Lou-Anne s’entraîne pour devenir championne cycliste. Chaque semaine, elle parcourt 23 kilomètres de plus que la semaine précédente.
À la fin de la sixième semaine, elle a parcouru en tout 837 kilomètres.

Combien a-t-elle parcouru de kilomètres la première semaine ?
(D’après le Rallye Mathématique Poitou-Charentes 1999)
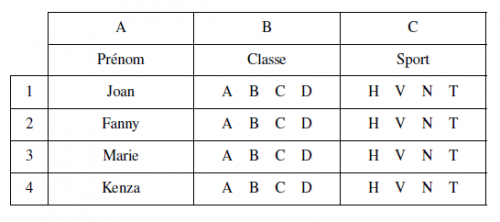
Au collège, 4 amies Joan, Fanny, Marie et Kenza sont dans quatre classes de 6ème différentes (A, B, C, D) et pratiquent quatre sports différents : handball, volley, natation et tennis.
• indice n◦1 : L’élève de 6ème A et l’élève de 6ème B ainsi que Joan ne manquent jamais les matchs de la handballeuse ;
• indice n◦2 : Fanny et Joan ont accompagné leur amie à la piscine mais l’élève de 6ème C n’est pas venue car elle avait des devoirs à faire ;
• indice n◦3 : Marie et la joueuse de tennis sont demi-pensionnaires alors que la nageuse et l’élève de 6ème B sont externes.
Retrouver les classes et les sports de chacune :
Un ballon de football possède 32 "faces" :
20 sont des "hexagones" (en blanc) et 12 sont des "pentagones" (en noir).

Dans l’opération suivante, chaque lettre représente toujours le même chiffre. Deux lettres différentes représentent deux chiffres différents. Aucun des nombres représentés par un mot ne commence par zéro.
| S | P | O | R | T | |||
| + | E | F | F | O | R | T |
| P | L | A | I | S | I | R |
Quatre amis sont dans une salle pour voir un match de volley-ball. Un gardien vérifie les billets d’entrée et constate qu’ils n’en ont que trois...
Il interroge les quatre amis pour savoir qui n’a pas payé son entrée :
Ce n’est pas moi, dit Samma.
C’est Robin, dit Julie.
C’est Basile, dit Robin.
Julie a tort, dit Basile.

Le gardien est sûr qu’un seul enfant ment.
Qui a menti ?
(D’après le Rallye Mathématique Poitou-Charentes 1993)
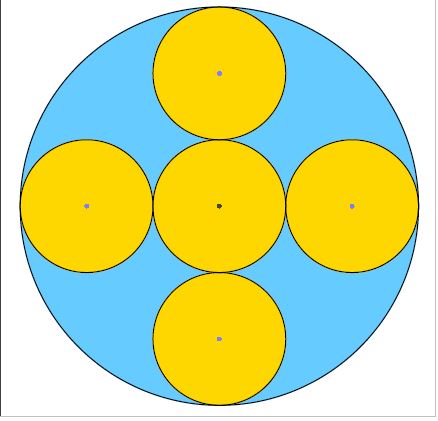
Cinq étuis cylindriques de balle de tennis (de couleur jaune) sont rangés dans un grand étui cylindrique (de couleur bleu).
L’étui central est tangent aux quatre autres étuis et chacun des quatre autres étuis est tangent au grand étui. Sachant que le fond du grand étui a une aire de 288 cm²,
Lors d’un spectacle de cirque, Adèle et ses amis ont assisté à une pyramide humaine de quatre étages. Ils sont impressionnés par la hauteur qu’atteint cette pyramide. Par un petit calcul, Adèle compte que pour obtenir une pyramide aussi haute que la tour Eiffel, il faudrait près de 200 étages.
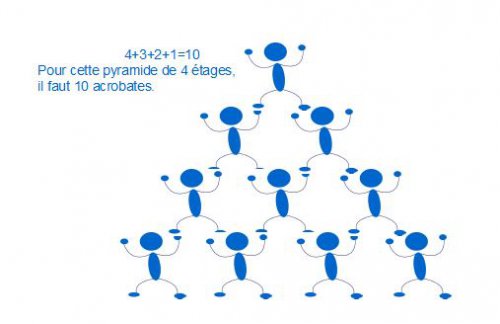
Combien faudrait-il d’acrobates pour construire une pyramide de 200 étages ?
Trois cyclistes démarrent ensemble et font le tour d’un vélodrome. On suppose qu’ils roulent tous à allure constante.
• le premier fait un tour en 1 minute 12 s ;
• Le deuxième fait un tour en 1 minute 15 s ;
• le troisième fait un tour en 1 minute 20 s.
Au bout de combien de temps franchissent-ils de nouveau ensemble la ligne d’arrivée ?
Pour les 6èmes et 5èmes
Abel suit le championnat du Monde de F1. Il étudie avec attention les tracés des différents circuits.
Pour ses voitures, il réfléchit à la construction d’un circuit contenu dans un rectangle de 3 sur 4 et utilisant les deux types d’éléments suivants :

Voici deux exemples de circuits :

Combien de circuits différents peut-il construire avec uniquement ces deux types d’éléments et en utilisant les 12 "cases" d’un rectangle de 3 sur 4 ? (sans laisser de "cases vides")
Pour les 4èmes et 3èmes
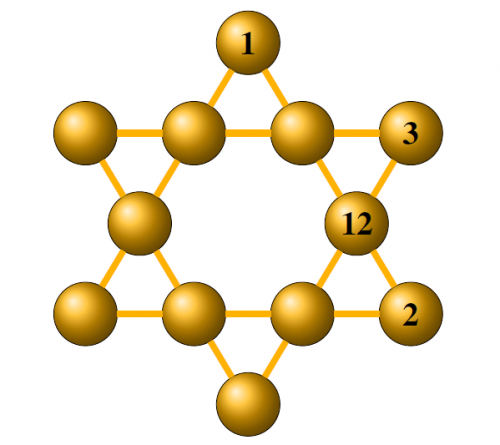
Dans les vestiaires, Antoine s’est amusé à placer les maillots des 12 joueurs de foot de son équipe (11 titulaires et 1 remplaçant) de telle sorte que la somme de 4 nombres alignés soit toujours la même.
Place les nombres de 4 à 11 dans les emplacements manquants.
Les solutions : cliquez ici
