Solutions des énigmes de la semaine des Mathématiques 2016 publié le 08/04/2016

Bravo à Emma P, élève de 6ème, qui a résolu une énigme de niveau 6ème/5ème, et essayé de répondre à une autre énigme de niveau 4ème/3ème.

• Si la première semaine elle fait 0 kilomètre :
La deuxième semaine, elle parcourt 23 kilomètres.
La troisième semaine, elle parcourt 46 kilomètres (23 + 23 = 23 × 2).
La quatrième semaine, elle parcourt 69 kilomètres (46 + 23 = 23 × 3).
La cinquième semaine, elle parcourt 92 kilomètres (69 + 23 = 23 × 4).
La sixième semaine, elle parcourt 115 kilomètres (92 + 23 = 23 × 5).
Dans ce cas, à la fin de la sixième semaine elle a parcouru 345 kilomètres (23 + 46 + 69 + 92 + 115).
• Nombre de kilomètres parcourus la première semaine :
En tout, elle a parcouru 837 kilomètres. Il lui manque donc 492 kilomètres.
Chaque semaine, elle parcourt les kilomètres de la semaine précédente. Donc il faut partager 492 en six.
Elle a parcouru 82 kilomètres la première semaine (492 ÷ 6).

Ce ballon compte 60 "sommets", ce sont en effet les "sommets" des 12 "pentagones".

Il faut commencer par rechercher l’enfant qui ment :
Comme Julie et Robin sont en désaccord, l’un des deux ment.
Comme Julie et Basile sont en désaccord, l’un des deux ment.
Finalement, comme un seul enfant ment, la seule possibilité est que Julie mente.
On en déduit que Robin dit vrai et que Basile n’a pas payé son billet.

Regardons de plus près comment nous aurions pu compter les 10 acrobates sans pour autant ajouter leur nombre par étage. Pour cela, plaçons les acrobates les uns sur les autres et complétons cette formation par un autre groupe de même composition d’acrobates verts afin de créer "un rectangle " de 5 acrobates sur 4 acrobates.

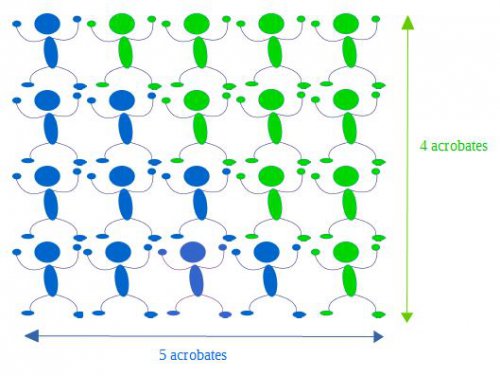
En tout, on a 20 acrobates. Les bleus ne sont que la moitié de ce groupe, soit 10 acrobates.
Regardons pour une pyramide de 10 étages : on complète de la même façon. On a donc "un rectangle " de 11 acrobates sur 10 acrobates.

Au total, 110 acrobates. Pour construire une pyramide de 10 étages, on a besoin de la moitié soit 55 acrobates.
Finalement, pour construire une pyramide de 200 étages on construit "un rectangle " de 201 acrobates sur 200 acrobates. Cela donne 40 200 acrobates.
Pour construire une pyramide de 200 étages, on a donc besoin de la moitié soit 20 100 acrobates.

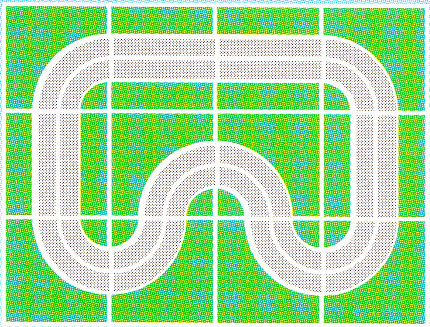
Regardons de plus près comment sont construits ces circuits. Si nous ne voulons avoir aucune "case vide", il faut nécessairement mettre un "virage" dans chacun des quatre coins. Cela laisse peu de choix pour la suite, il faut forcément mettre "une ligne droite" dans la première et la dernière colonne.
Finalement, il n’existe qu’une unique solution :

• Joan n’est pas en 6ème A ni en 6ème B (indice 1) ni en 6ème C donc elle est en 6ème D.
• La nageuse n’est ni Joan ni Fanny (indice 2) ni Marie (indice 3), c’est donc Kenza.
• L’élève de 6ème B ne fait pas de handball (indice 1), ni de natation (indice 3) ni de tennis (indice 3), elle fait donc du volley.
• Joan ne peut donc pas être volleyeuse car elle est en 6 ème D. Elle n’est ni handballeuse (indice 1) ni nageuse (indice 2) elle est donc joueuse de tennis. Joan est donc en 6ème D et fait du tennis.
• La handballeuse n’est ni en 6ème A ni en 6ème B (indice 1) ni en 6ème D (c’est Joan) donc elle est en 6ème C. La nageuse est donc en 6ème A et c’est Kenza. Kenza est donc en 6ème A et fait de la natation.
• La volleyeuse n’est pas Joan (indice 1) ni Marie (indice 3) ni Kenza (nageuse) donc c’est Fanny qui est en 6ème B. Fanny est donc en 6ème B et fait du volley.
• il reste donc Marie qui est en 6ème C et fait du handball.

il n’y a qu’une solution :

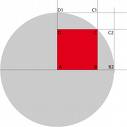
Le rayon (R) de l’étui bleu est est trois fois plus grand que le rayon (r) de l’étui jaune.
Ainsi, l’aire de l’étui jaune est 9 fois plus petite que l’aire de l’étui bleu. (On peut aussi utiliser la formule de l’aire d’un disque : et remplacer R par 3r pour s’en rendre compte.)
L’aire d’un étui jaune est donc : 32cm²

On transforme les durées en secondes et on obtient respectivement : 72, 75, 80 secondes.
Ensuite, il faut trouver le Plus Petit Multiple Commun strictement positif (PPCM) à ces trois nombres :
On trouve 3600.
Ils franchissent de nouveau ensemble la ligne d’arrivée au bout d’une heure.

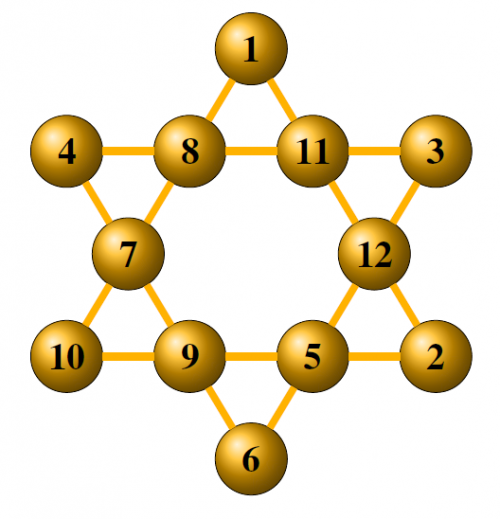
Notons S la somme commune à tous les alignements : il y a 6 alignements et chaque nombre fait partie de 2 alignements donc 6S = 2 × (1 + ..... + 12) soit S = 26 donc 1, 12 et 2 sont alignés avec 11 pour faire 26.
Dans l’alignement du 12 et du 3, 12+3=15 donc il faut faire 11 en deux nombres 11 = 4 + 7 = 5 + 6 (le 1, le 2 et le 3 étant déjà placés).
Dans l’alignement du 3 et du 11, 11+3=14 donc il faut faire 12 en deux nombres 12 = 4 + 8 = 5 + 7 (le 1, le 2 et le 3 étant déjà placés). On est obligé d’aligner le 8 avec le 1 sinon, on ne peut pas faire 26. On est obligé d’aligner le 5 avec le 2 sinon, avec le 6, il resterait 18 à faire en deux nombres et il ne reste que 7 9 et 10 à placer : impossible.
Les trois emplacements se déduisent facilement :

Pour voir les énoncés des énigmes, cliquez ici.