Solutions des énigmes de la semaines des Mathématiques 2012 publié le 06/09/2014
[**Solutions des énigmes de la semaine des Mathématiques*]
Retrouvez la liste des énigmes en cliquant ici
Pour les élèves de 6ème et 5ème
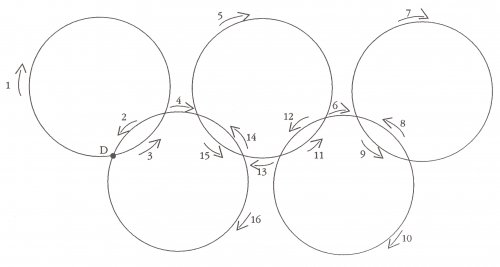
**Lundi 12 mars : les Jeux Olympiques
Voici un tracé possible : les arcs sont tracés dans l’ordre suivant les flèches.
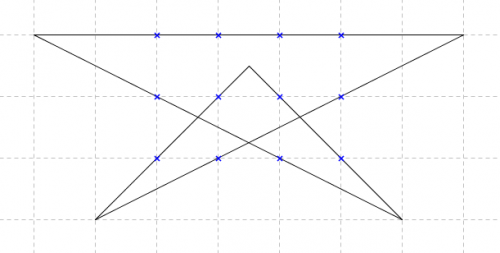
**Mardi 13 mars : les douze points
**Mercredi 14 mars : La station service
• Mesurer 4 litres
On remplit à ras bord le récipient de 11 litres.
On verse le contenu de ce récipient dans celui de 13 litres.
Dans le récipient de 13 litres, on pourrait encore verser 2 litres.
On remplit à ras bord le récipient de 6 litres.
On verse 2 litres de ce récipient dans celui de 13 litres qui contient déjà 11 litres.
Il reste alors 4 litres dans le récipient de 6 litres.
• Mesurer tout nombre entier de litres
Si on arrive à mesurer 1 litre, on pourra mesurer tout nombre entier de litres.
En effet pour mesurer n litres, il suffit de répéter la mesure de 1 litre n fois.
Par exemple, pour mesurer 9 litres, il suffit de mesurer 9 fois 1 litre.
• Mesurer 1 litre
On remplit à ras bord le récipient de 6 litres.
On verse ce récipient dans celui de 11 litres.
On remplit à nouveau à ras bord le récipient de 6 litres.
On verse ce récipient dans celui de 11 litres qui contenait déjà 6 litres.
On a donc versé seulement 5 litres.
Il reste donc 1 litre dans le récipient de 6 litres.
**Jeudi 15 mars : Le gâteau d’anniversaire
• Découpe du gâteau
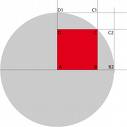
On choisit un point vers le centre du gâteau qui se trouve à moins de 17 cm des 4 sommets ; il est noté E sur la figure ci-dessous.
On coupe le gâteau en partant de E jusqu’à chacun des 4 sommets.
La première jumelle mangera les deux parts vertes AEB et CDE et la deuxième jumelle mangera les deux autres parts bleues BCE et ADE.
Ce partage est équitable !
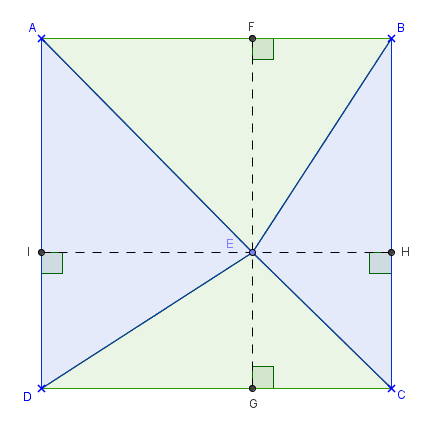
• Justification de l’égalité des parts
Imaginons que les droites parallèles aux côtés du carré qui passent par E soient tracées.
La première coupe le côté [AB] en F et le côté [CD] en G.
La deuxième coupe le côté [BC] en H et le côté [AD] en I.
Les quadrilatères AFEI, BHEF, CGEH et DIEG sont des rectangles partagés en deux triangles rectangles de mêmes aires par l’une de leurs diagonales.
Aire(ABE) + Aire(CDE) = Aire(AEF) + Aire(BEF) + Aire(CEG) + Aire(DEG)
Aire(ABE) + Aire(CDE) = Aire(AEI) + Aire(BEH) + Aire(CEH) + Aire(DEI)
Aire(ABE) + Aire(CDE) = Aire(AEI) + Aire(DEI) + Aire(BEH) + Aire(CEH)
Aire(ABE) + Aire(CDE) = Aire(ADE) + Aire(BCE)
**Vendredi 16 mars :La somme assommante
• Les sept solutions
576 + 9 658 = 10 234.
675 + 9 658 = 10 243.
748 + 9 875 = 10 623.
847 + 9 785 = 10 632.
586 + 9 657 = 10 243.
874 + 9 482 = 10 356.
758 + 9 874 = 10 632.
Pour les élèves de 4ème et 3ème
**Lundi 12 mars : Le tableau effacé
• Comptage
Lorsqu’on écrit sur le tableau les vingt nombres entiers dans l’ordre croissant de 1 à 20, on peut alors compter 31 chiffres.
On doit en effacer 20 ; il restera donc un nombre de 11 chiffres inscrit sur le tableau.
• Chiffre des dizaines de milliards du plus grand nombre possible
Si on veut le plus grand nombre possible, son premier chiffre devra être un 9.
Il y a seulement deux fois le chiffre 9 dans notre liste et le deuxième (celui de 19) est beaucoup "trop loin".
On doit donc effacer les huit premiers chiffres pour faire commencer notre nombre par 9.
On a effacé huit chiffres ; il nous en reste donc douze à effacer (20 - 8 =12).
• Chiffre des unités de milliards du plus grand nombre possible
Pour avoir le plus grand nombre possible inscrit sur le tableau, on doit chercher à avoir le plus grand chiffre possible en deuxième position.
Les chiffres 9, 8, 7, 6 sont "trop loin" car il faudrait effacer plus de douze chiffres pour les atteindre.
Par contre, en effaçant onze chiffres, on obtient un 5 comme deuxième chiffre de notre nombre inconnu.
• Chiffre des centaines de millions du plus grand nombre possible
On avait effacé huit chiffres au début et maintenant, on vient d’en effacer onze ; il nous en reste plus qu’un à enlever.
Pour avoir le plus grand nombre possible inscrit sur le tableau, il nous reste à enlever le 1 qui suit le 5 qu’on a gardé.
De cette façon, le troisième chiffre du nombre restant inscrit au tableau sera un 6.
• Le plus grand nombre possible
Chaque chiffre effacé a été remplacé par un tiret.
- - - - - - - 9 - - - - - - - - - - - 5 - 617181920
Le plus grand nombre obtenu est donc 95 617 181 920.
**Mardi 13 mars : Le cube truffé
Le grand cube comprend 512 petits cubes (8x8x8)
Il y a 17 rangées de cubes noirs :
mais 9 cubes noirs sont comptabilisés 2 fois et 1 cube noir l’est 3 fois.
Finalement, il y a 125 cubes noirs et 387 cubes blancs.
**Mercredi 14 mars : Au feu les pompiers !
Le pompier se tient sur l’échelon du milieu de l’échelle, il y a donc autant d’échelons au-dessus qu’au dessus ; l’échelle possède donc un nombre impair d’échelons.
Les montées et descentes successives de l’énoncé font finalement monter le pompier de 13 échelons.
L’échelle possède donc 27 échelons (13x2+1)
**Jeudi 15 mars : Les allumettes
Avec 12 allumettes, on peut former le célèbre triangle rectangle dont les côtés mesurent 3, 4 et 5.
Il est alors possible de diminuer l’aire de ce triangle en "retirant" 3 carrés.
Voici une disposition possible :
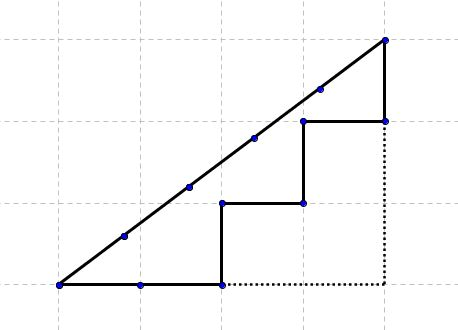
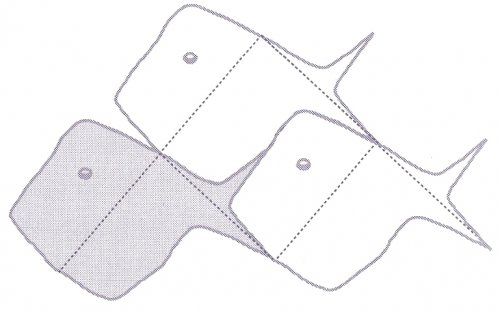
**Vendredi 16 mars : Poisson à la découpe
Ce poisson permet de réaliser un pavage du plan. Ce pavage nous suggère alors un découpage qui convient.